MATH5824 Generalised Linear and Additive Models

4.1 Overview

In Section 1.3 we described a general statistical model with a response variable \(y\) and an explanatory variable \(x\). We observe \(y_i\) at each location \(x_i,\) for \(i=1,\ldots, n\). We imagined that the \(y\)’s are noisy versions of a smooth function of \(t\), say \(f(\cdot)\) where the errors follow a normal distribution with constant variance. That is \[ y_i = f(x_i) + \epsilon_i, \quad \epsilon_i \sim \mathrm{N}(0,\sigma^2), \] for \(i=1,\ldots,n\), where \(f\) is smooth, the \(\epsilon_i\) are i.i.d., and \(f\) and \(\sigma^2\) are unknown.
The log-likelihood for this situation is: \[ l(f; \mathbf{y}) = -\frac{1}{2\sigma^2} \sum_{i=1}^n \left(y_i - f(x_i)\right)^2 - n \log \sigma \tag{4.1}\] and we wish to estimate \(f\) for a given data set \(\mathbf{y}=\{y_1,\dots, y_n\}\). With no constraints on \(f\), the log-likelihood would be maximised by setting \(f(x_i)=y_i\) for all \(i\), and we would estimate the noise variance as \(\hat{\sigma}^2=0\). This takes no account of randomness in the data and \(f\) would in general need to be quite wiggly to achieve this fit.

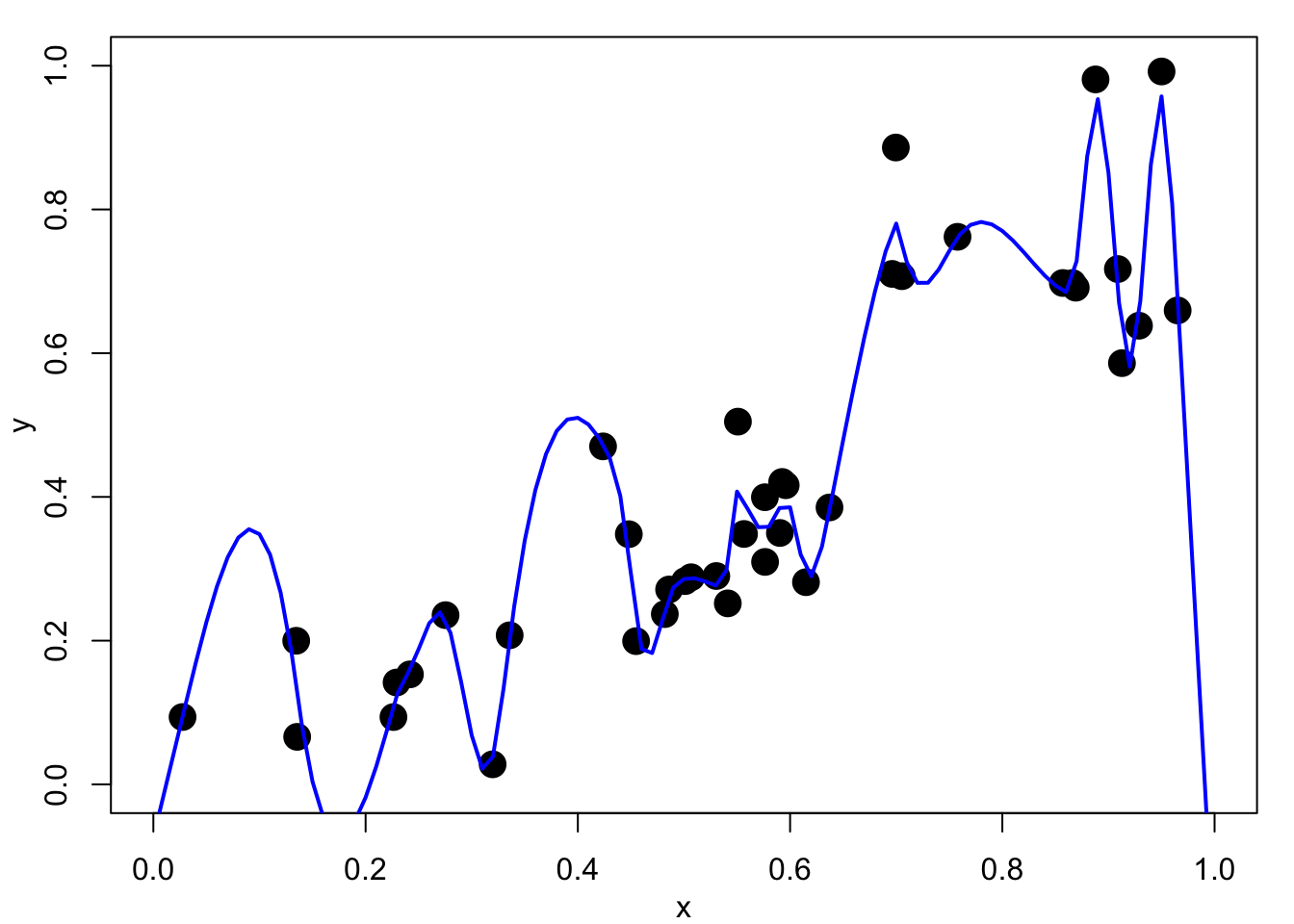
Figure 4.1 (a) shows such an interpolation of noisy data. This would be of little use for explanation, interpolation or prediction.

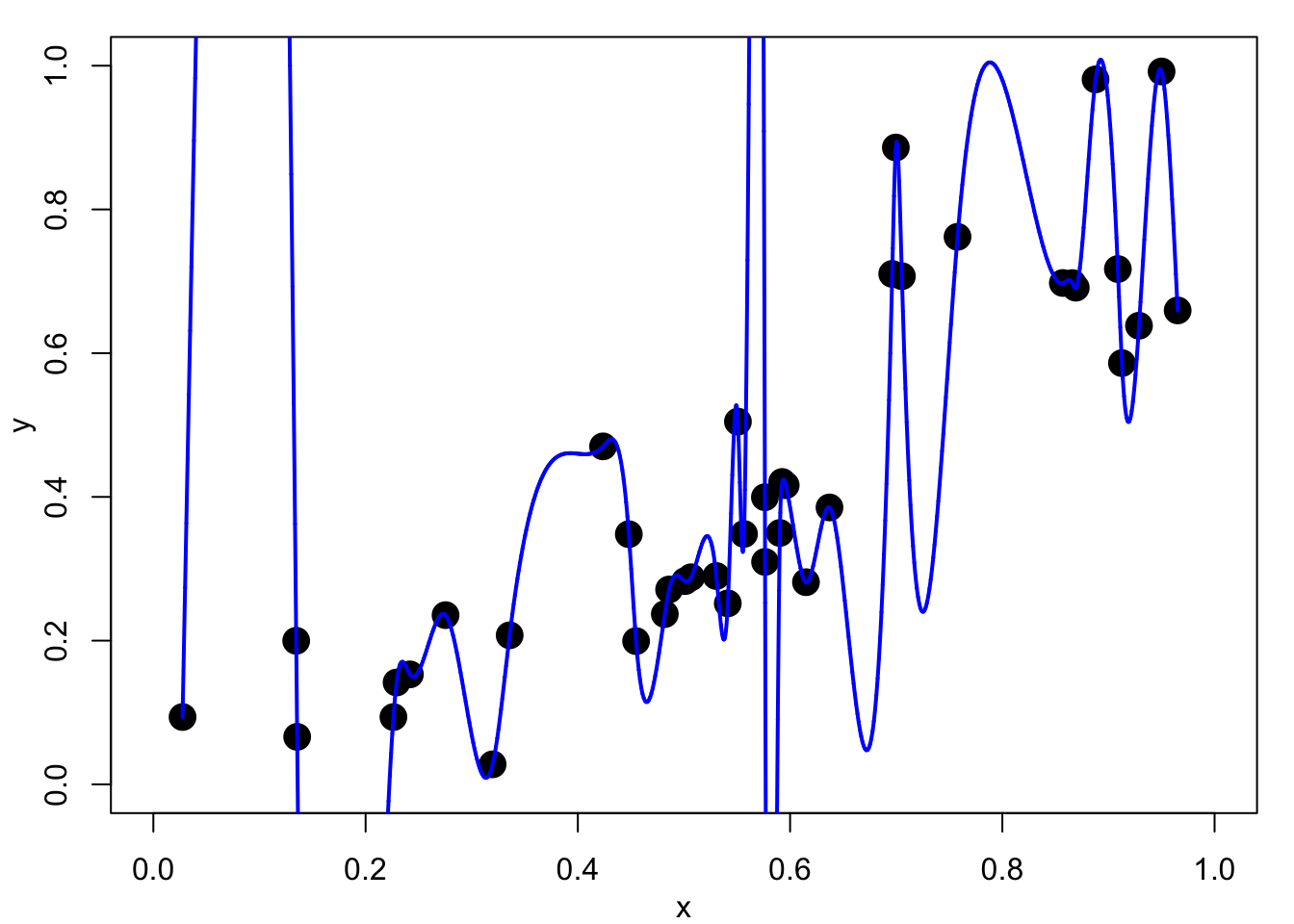
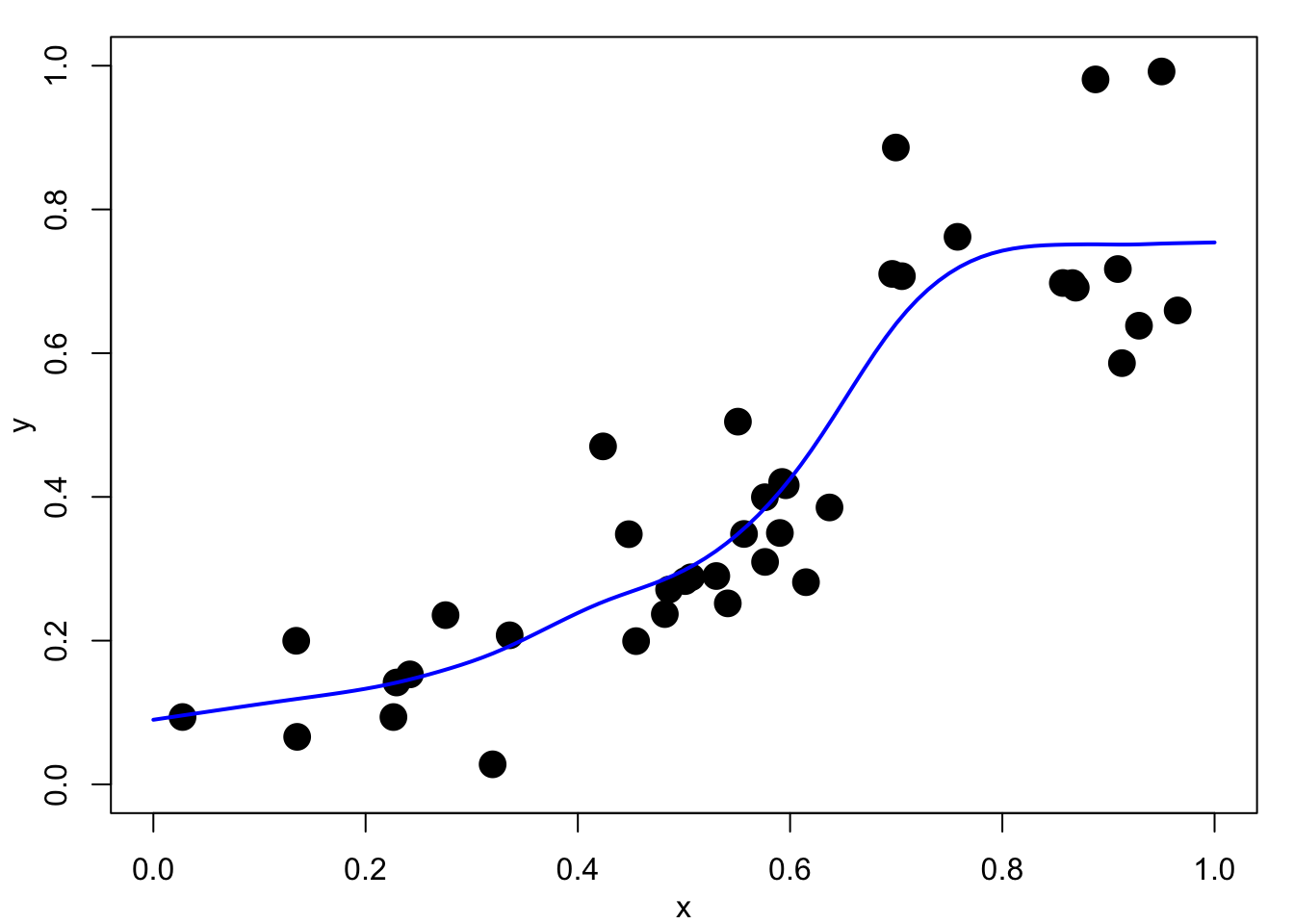
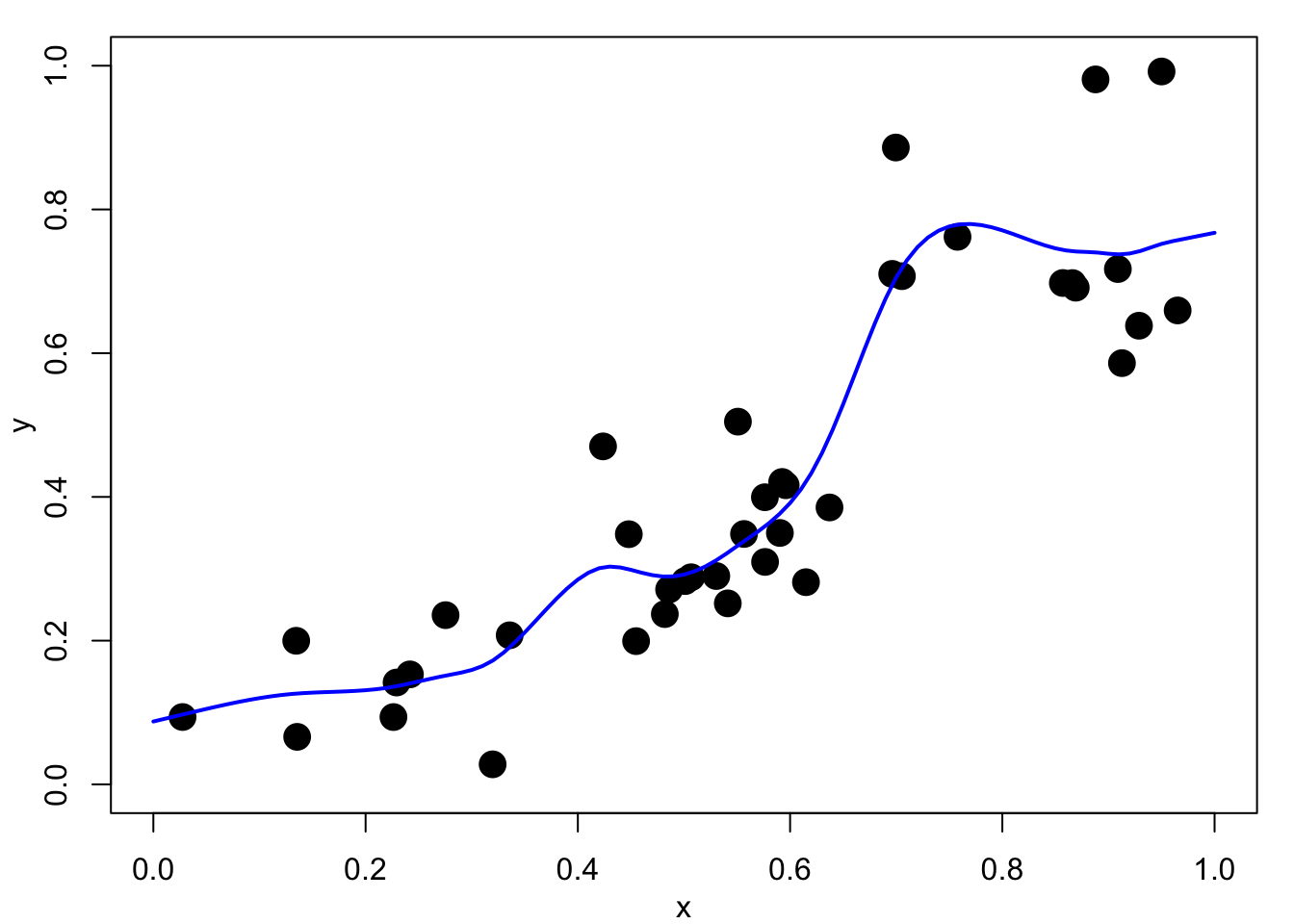
We do not expect, or even want, the fitted function \(f\) to pass exactly through the data points \(\{(x_i,y_i), i=1,\dots,n\}\), but merely to lie close to them. We would rather trade-off goodness-of-fit against smoothness of \(f\). Figure 4.1 (b) shows a smoothing spline fit to the same data. This is much better as there is a clear explanation of the relationship, it could be used reasonably well for interpolation and prediction.

4.2 The penalised least-squares criterion

Noting that maximizing Equation 4.1 is equivalent to minimizing the residual sum of squares: \(\sum_{i=1}^n \left(y_i - f(x_i)\right)^2\), we can achieve this trade-off by minimizing a penalised sum of squared residuals: \[ R_\nu(f,\lambda) = \sum_{i=1}^n \left(y_i - f(x_i)\right)^2 + \lambda J_\nu(f), \tag{4.2}\] where \(J_\nu(f)\), as first defined in Equation 3.8, penalizes the roughness of \(f\). The smoothing parameter \(\lambda\geq 0\) controls the severity of this penalty. For now we will assume \(\lambda\), which absorbs the \(\sigma^2\) in Equation 4.1, is known.

Figure 4.2 shows example smoothing spline fits using a range of smoothing parameters, \(\lambda\). In Figure 4.2 (a) the fit is essentially a straight line, perhaps Figure 4.2 (b) and Figure 4.2 (c) show acceptable fits. Figure 4.2 (d), with a very small \(\lambda\) value is close to an interpolating spline fit and is clearly unacceptable.

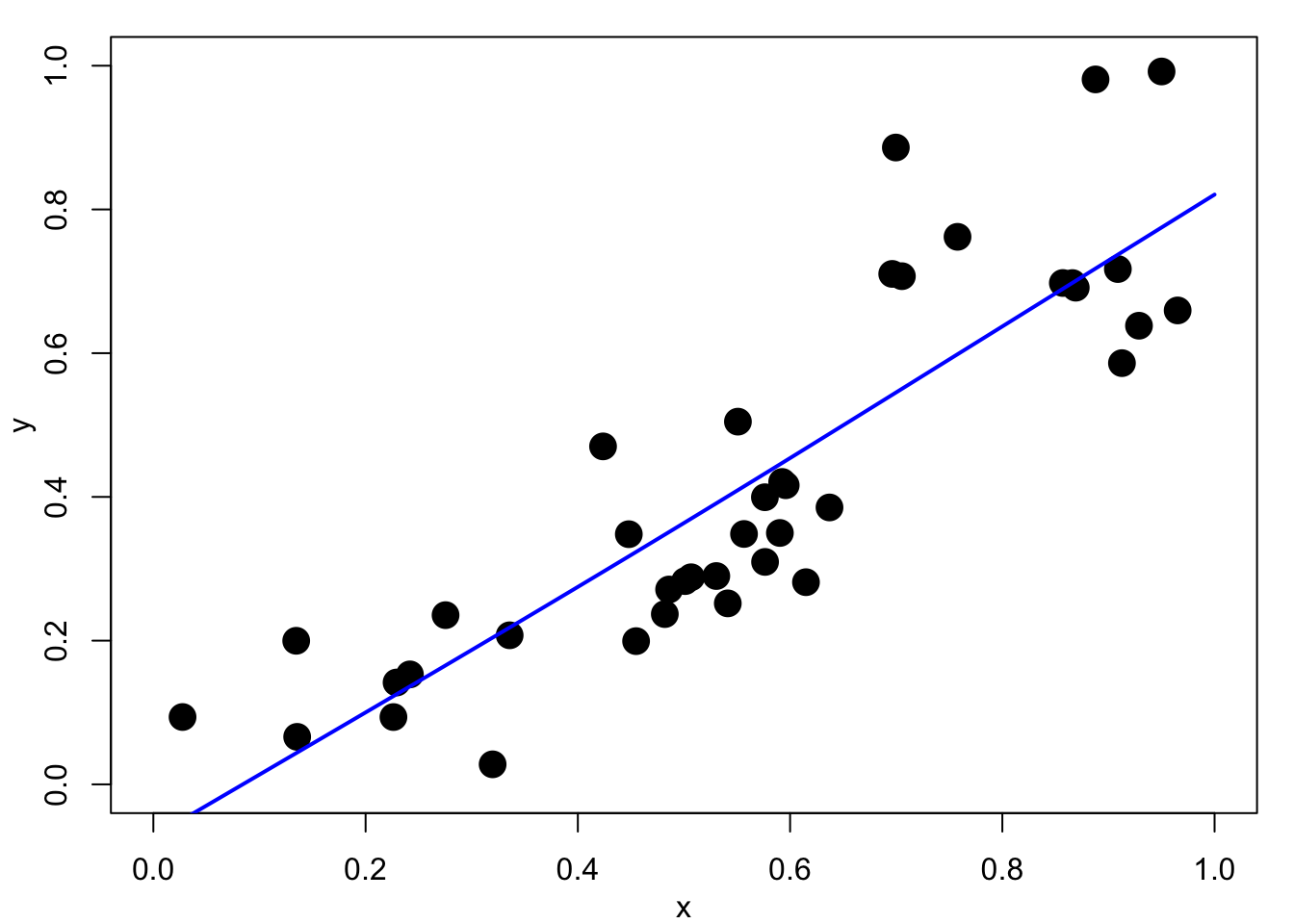
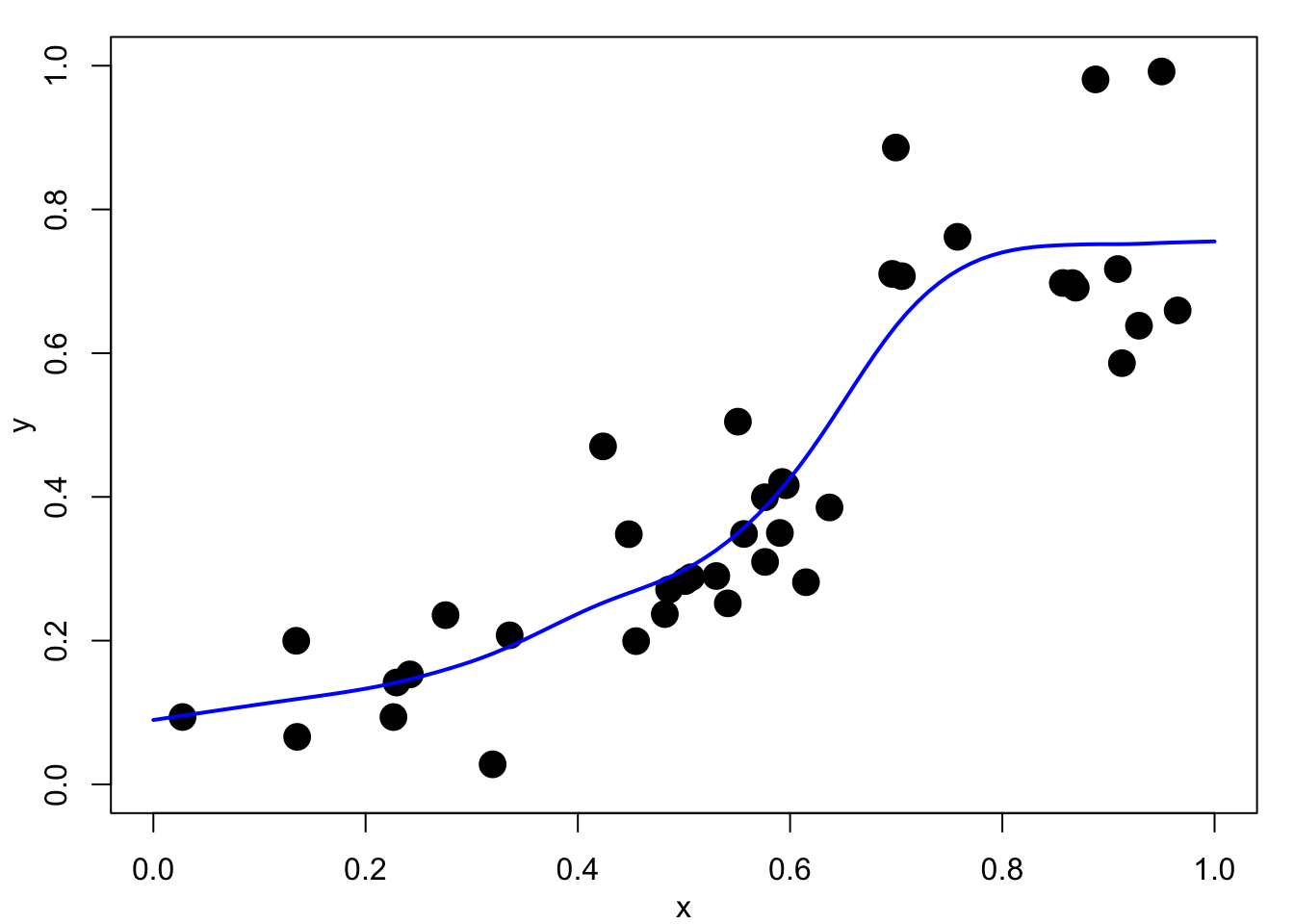
As the smoothing parameter \(\lambda\) increases, the optimal \(f\) becomes smoother. In particular, it can be shown that as \(\lambda \rightarrow \infty\), the vector of coefficients \({\mathbf b} \rightarrow {\mathbf 0}\), and \({\mathbf a}\) tends to the usual least-squares estimate of the regression parameters. Thus, the smoothing spline converges to the sample mean \(f(x)=\bar y\) when \(\nu=1\), and to the ordinary least squares fitted line, \(f(x)=\hat\alpha+\hat\beta t\), when \(\nu=2\). In the other direction, as \(\lambda \rightarrow 0\) the smoothing solution converges to the interpolating spline.

Focus on smoothing splines quiz

Test your knowledge recall and comprehension to reinforce basic ideas about smoothing splines.

Which of the following statements is NOT true?
The smoothing spline parameter λ controls the amount of smoothing Interpolating splines pass through all data points Smoothing splines should be used for all problems Smoothing splines are better for noisy data Both interpolating and smoothing splines are piecewise polynomial functions

2 Which of the following statements is true about splines?

Which of the following best describes the result of using a very large value of λ in a cubic smoothing spline?
Which of the following best describes the result of using a very small value of λ in a linear smoothing spline?
Which of the following statements best describes how to choose the value of λ?

4.3 Relation to interpolating splines

We show in the following proposition that the function \(f\) which minimizes Equation 4.2 is the interpolating spline of its fitted values.

Proposition 4.1 Suppose \(\hat{f}\) minimizes \(R_\nu(f,\lambda)\) and let \(\hat{y}_i = \hat{f}(x_i), i=1,\dots,n\) denote the corresponding fitted values. Then, \(\hat{f}\) solves the interpolation problem for the artificial data set \((x_i,\hat{y}_i), i=1,\dots , n\). That is, \(\hat{f}\) minimizes \(J_\nu(f)\) over functions \(f\) satisfying \(\hat f(x_i)=\hat{y}_i\), \(i=1,\ldots,n\). Consequently, \(\hat{f}\) is a \(p^{\text{th}}\)-order natural spline, where \(p=2\nu-1\). This means that, when solving the smoothing problem, we only need consider spline functions given by the representations in Proposition 3.1.

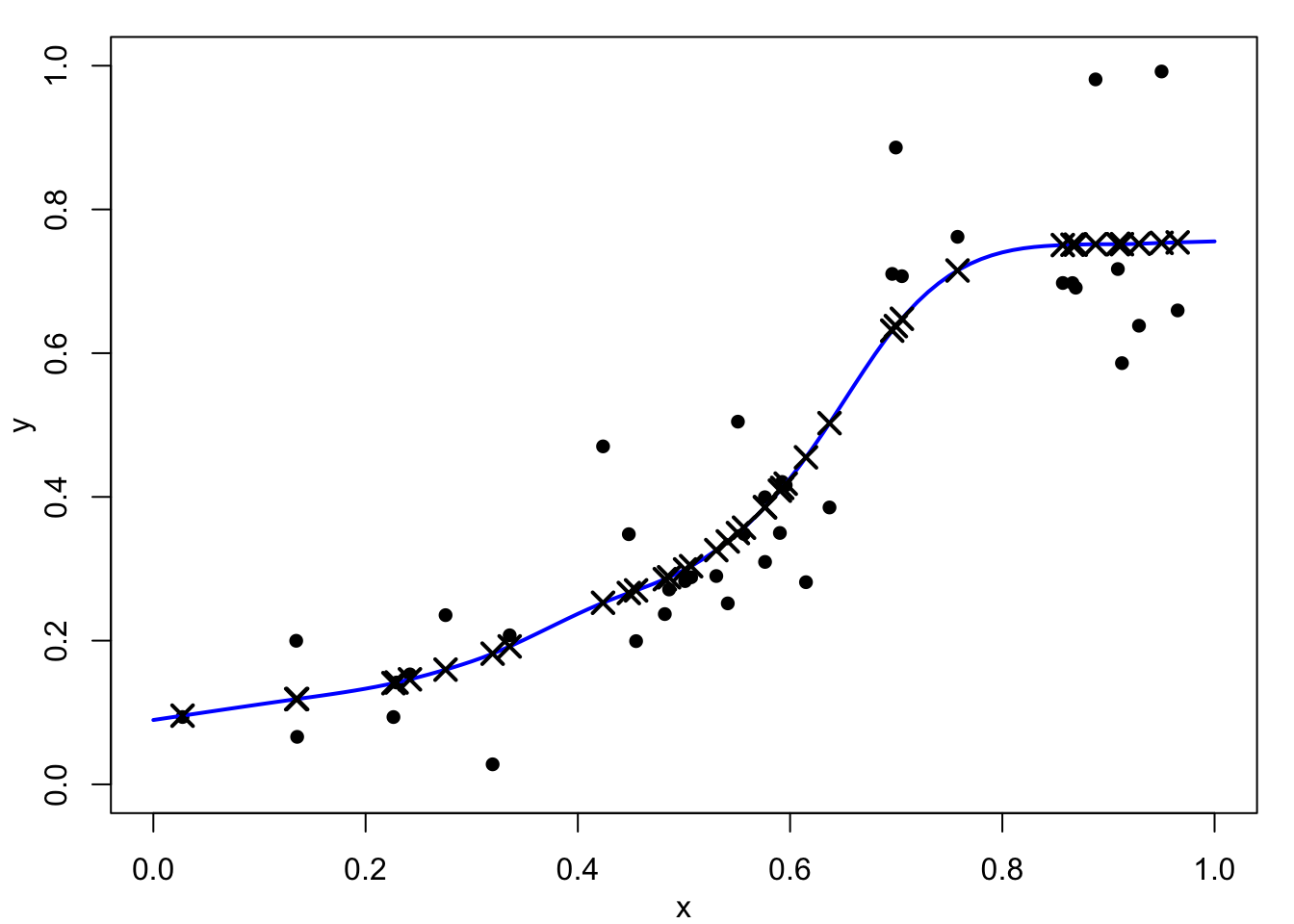
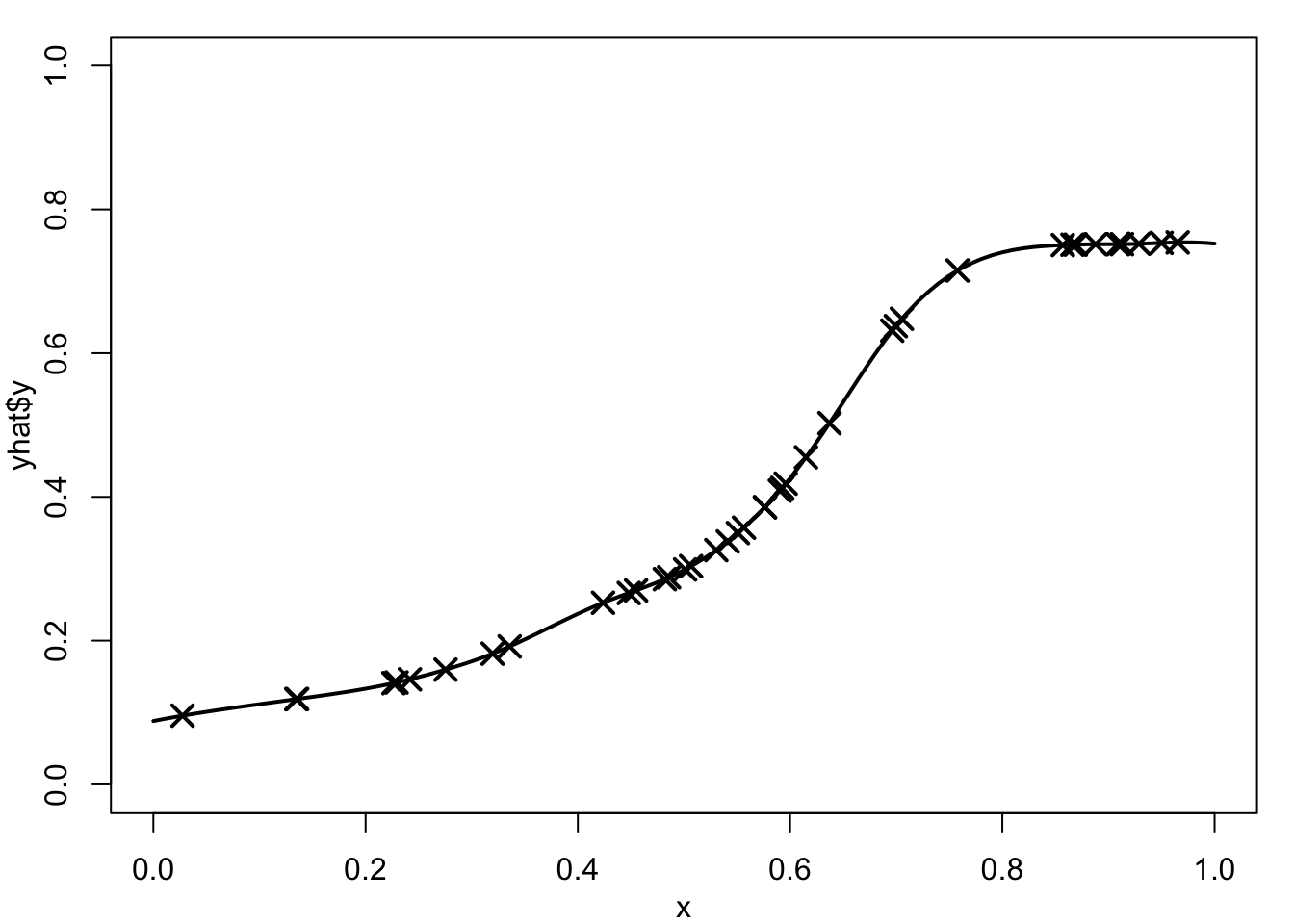
(a) Smoothing spline of data shown as dots and with fitted values shown as crosses

Proof: Suppose the assertion is not true. In this case, we must be able to find a function \({\hat{f}^\star}\), say, which also interpolates the artificial data \((x_i,\hat{y}_i), i=1,\dots ,n\), but which has a smaller roughness penalty. That is \[ J_\nu({\hat{f}^\star}) < J_\nu(\hat{f}) \mbox{ with } \hat{f}^\star(x_i) = \hat{y}_i, \ i=1,\ldots,n. \] Note that the fitted values from the function \(\hat f^\star\) are also equal to \(\hat y_i, i=1,\dots,n\) as it interpolates the same artificial data as \(\hat f\).

Now, from Equation 4.2, \[\begin{align*} R_\nu(\hat{f}^\star, \lambda) &= \sum_i (y_i-\hat{y}_i)^2 + \lambda J_\nu(\hat{f}^\star)\\ &< \sum_i (y_i-\hat{y}_i)^2 + \lambda J_\nu(\hat{f}) = R_\nu(\hat{f}, \lambda). \end{align*}\] Hence \(R_\nu(\hat{f}^\star, \lambda) < R_\nu(\hat{f}, \lambda)\). But, by construction \(\hat{f}\) minimizes \(R_\nu(f, \lambda),\) which is a contradiction. Hence, it must not be possible to find a function \({\hat{f}^\star}\) which also interpolates the artificial data but which has a smaller roughness penalty.

We have shown that \(\hat{f}\) is the optimal interpolant of the fitted values \(\hat{y}_i,\ i=1,\dots,n,\) so it follows from Proposition 4.1 that \(\hat{f}\) is a natural spline of order \(p=2\nu-1\).

4.4 The smoothing problem in matrix notation

We have just proved that the function \(\hat{f}\) that minimizes \(R_\nu (f, \lambda)\) must be a natural spline (linear if \(\nu=1\), cubic if \(\nu=2\)) with knots at \(\{t_i,\,i=1,\ldots,n\}.\) That is, as in Proposition 3.1, we can write:

\[ \hat{f}(t) = \sum_{i=1}^n b_i\left|t-t_i\right|^p + \begin{cases} a_0, &\nu=1\\ a_o + a_1t, &\nu=2, \end{cases} \tag{4.3}\] where \(p=2\nu-1\) and constraints \[ \sum_{i=1}^n b_i = 0 \, \mbox{ for }\, \nu=1 \quad \sum_{i=1}^n b_i = \sum_{i=1}^n b_i \, t_i = 0 \, \mbox{ for }\, \nu=2. \tag{4.4}\]

However, we have not yet figured out how to calculate the parameter values \(\hat{a}_0,\dots,\hat{a}_{\nu-1},\ \hat{b}_1,\dots,\hat{b}_n\) in Equation 4.3 which optimally fit the data \(y_1,\dots,y_n\). For this, it is convenient to re-express the penalised sum of squared residuals Equation 4.2 in matrix notation.

Proposition 4.2 The roughness of a natural linear spline \((\nu=1\), i.e. \(p=1)\) is \[ J_1(f) = -2\sum_{i=1}^n \sum_{k=1}^n b_i b_k \left| t_i - t_k \right| = c_1\,{\mathbf b}^T \, K_1 \, {\mathbf b}, \tag{4.5}\] and the roughness of a natural cubic spline (\(\nu=2\), i.e. \(p=3\)) is \[ J_2(f) = 12\sum_{i=1}^n \sum_{k=1}^n b_i b_k \left| t_i - t_k \right|^3 = c_2\,{\mathbf b}^T \, K_2 \, {\mathbf b}, \tag{4.6}\] where the constants are given by \[ c_1=-2, \quad c_2=12. \tag{4.7}\] Here \({\mathbf b}=(b_1,\ldots,b_n)^{T}\) is the vector of spline coefficients and \(K_\nu\) is the \(n\times n\) matrix whose \((i,k)\)th element is \(\left| t_i - t_k \right|^p\), where \(p=2\nu-1\) that is \[ K_\nu = \begin{bmatrix} |t_1-t_1|^p & |t_1-t_2|^p & \dots & |t_1-t_n|^p \\ |t_2-t_1|^p & |t_2-t_2|^p & \dots & |t_2-t_n|^p \\ \vdots & \vdots &\ddots & \vdots \\ |t_n-t_1|^p & |t_n-t_2|^p & \dots & |t_n-t_n|^p. \end{bmatrix} \]

Proof: To be covered later if there is sufficient time.

From Proposition 4.2 the roughness penalty satisfies: \[\begin{align} J_\nu (\hat{f}) = c_\nu \, {\mathbf b}^T K_\nu {\mathbf b} \label{eq:Jnufhat} \end{align}\] where \(c_1=-2\); \(c_2= 12\); \({\mathbf b}=(b_1,\ldots,b_n)^T\); and \(K_\nu\) is the \(n \times n\) matrix whose \((i,k)\)th element is \(\left|t_i-t_k\right|^p\).

From Equation 4.3, the value of \(\hat{f}\) at knot \(t_k\) is \[ \hat{f}(t_k) = \sum_{i=1}^n b_i\left|t_k-t_i\right|^p + \begin{cases}a_0, &\nu=1\\ a_0 + a_1t_k, &\nu=2 \end{cases}. \tag{4.8}\]

In matrix form, this is \[ \mathbf{\hat{f}} = \left[ \begin{array}{c}\hat{f}(t_1) \\ \vdots \\ \hat{f}(t_n)\end{array} \right] = K_\nu {\mathbf b} + L_\nu \mathbf{a}_{\,\nu} \tag{4.9}\] where \[ L_1 = \left[ \begin{array}{c} 1\\ \vdots \\ 1\end{array}\right], \quad \mathbf{a}_1 = a_0, \quad \quad \mbox{and} \quad \quad L_2 = \left[ \begin{array}{cc} 1 & t_1 \\ \vdots & \vdots \\ 1 & t_n \end{array} \right], \quad \mathbf{a}_2 = \left[\begin{array}{l}a_0\\a_1\end{array} \right] . \]

Thus, from Equation 4.4 – Equation 4.9, the penalised least-squares criterion Equation 4.2 reduces to a quadratic function of the parameters \(\mathbf{a}\) and \({\mathbf b}\):

\[ R_\nu(f, \lambda) = (\mathbf{y} - K_\nu \, {\mathbf b} - L_\nu \, \mathbf{a})^T (\mathbf{y} - K_\nu \, {\mathbf b} - L_\nu \, \mathbf{a}) + \lambda \,c_\nu \,{\mathbf b}^T K_\nu \,{\mathbf b} \tag{4.10}\] subject to \[ L_\nu^T\,{\mathbf b} = 0, \tag{4.11}\] where \(\mathbf{y} = (y_1,\ldots,y_n)^T\).

To find the explicit values for \(\mathbf{b}\) and \(\mathbf{a}\), we must minimize the quadratic function Equation 4.10 subject to the linear constraints Equation 4.11.

Proposition 4.3 The solution to the smoothing spline problem is given by \[ \begin{bmatrix} \hat{\mathbf a} \\ \hat{\mathbf b} \end{bmatrix} = \begin{bmatrix} 0 & L_\nu \\ L_\nu^T & K_\nu+\lambda^* I_n \end{bmatrix}^{-1} \begin{bmatrix} {\mathbf 0} \\ {\mathbf y} \end{bmatrix} \tag{4.12}\] and \(\lambda^* = c_\nu \lambda\).

Proof: Omitted.

4.5 Smoothing splines in R

Fitting a smoothing spline to data involved estimating values of \(\mathbf a\) and \(\mathbf b\) to minimize the penalised roughness measure in Equation 4.10 subject to the constraints in Equation 4.11 which yields the explicit equation in Equation 4.12.

Of course, it is possible to code the solution of this matrix system, but it is usual instead to use in-built commands in software such as R.

In R the basic command is:

Code

smooth.spline(x, y, lambda)

where \(\texttt{x}\) and \(\texttt{y}\) are vectors of data coordinates, and \(\texttt{lambda}\) specifies the value of the smoothing parameter to use – note that the effect of a given value of \(\lambda\) depends on the problem considered.

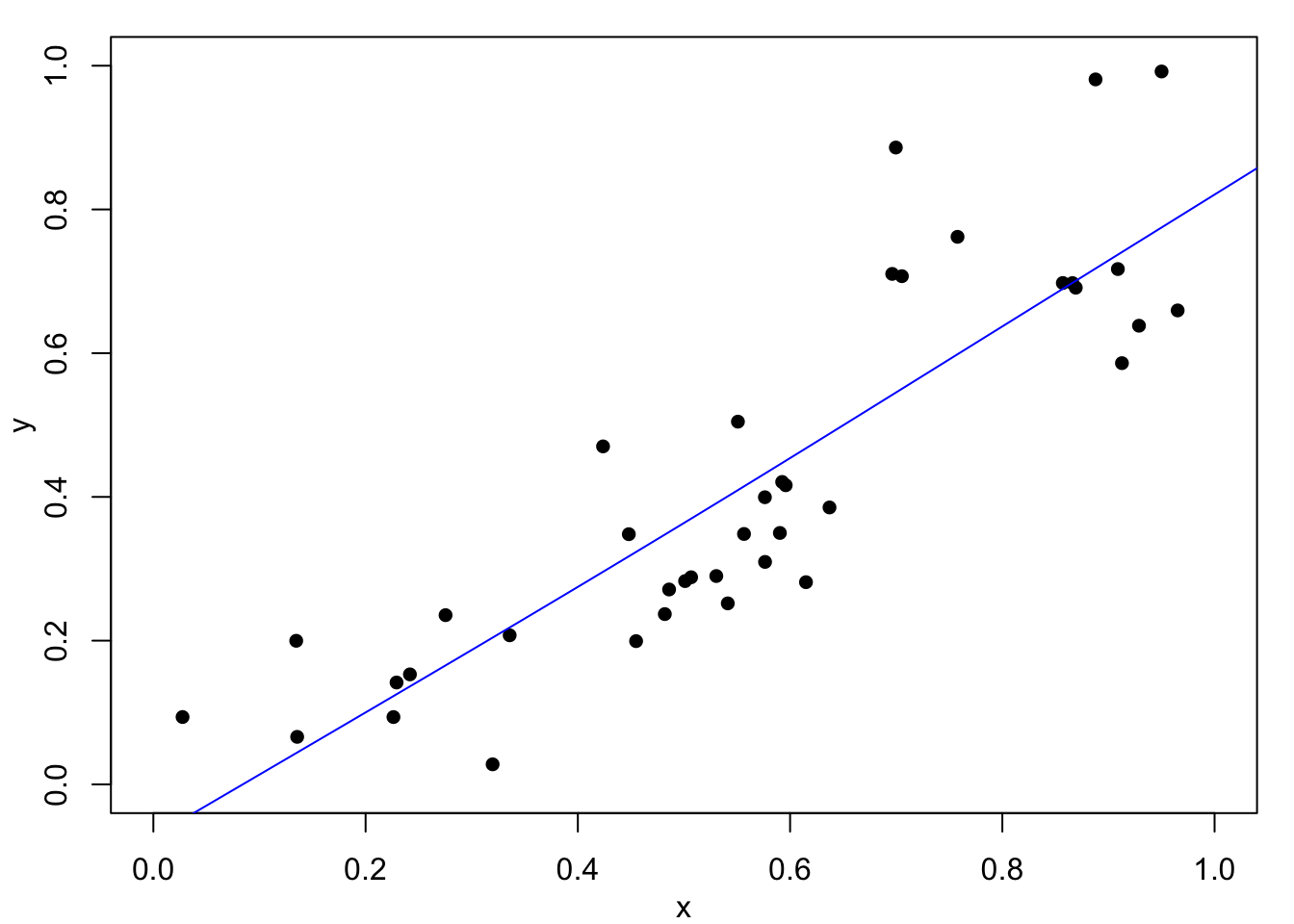
For example, consider the synthetic data set which contains a break-point at \(x=2/3\) first met in Figure 1.2. Fitted spline curves with \(\lambda=0.0001\) and \(\lambda=1\), shown in Figure 4.4, are based on the following commands:

Code

myfit1 = smooth.spline(x, y, lambda = 0.00001)
myfit2 = smooth.spline(x, y, lambda = 1)

Code

par(mar=c(3,3,1,1), mgp=c(2,1,0))
set.seed(12341)

x = runif(40)
y = 0.75*(x >= 0.67) + 0.6*x*(x<0.67) + rnorm(40,0,0.1)

plot(x,y, xlim=c(0,1), ylim=c(0,1), pch=16)
myfit1 = smooth.spline(x, y, lambda = 0.00001)
fit.locations = seq(0,10,0.01)
fitted = predict(myfit1, fit.locations)
lines(fitted, col="blue")

plot(x,y, xlim=c(0,1), ylim=c(0,1), pch=16)
myfit2 = smooth.spline(x, y, lambda = 1)
fit.locations = seq(0,10,0.01)
fitted = predict(myfit2, fit.locations)
lines(fitted, col="blue")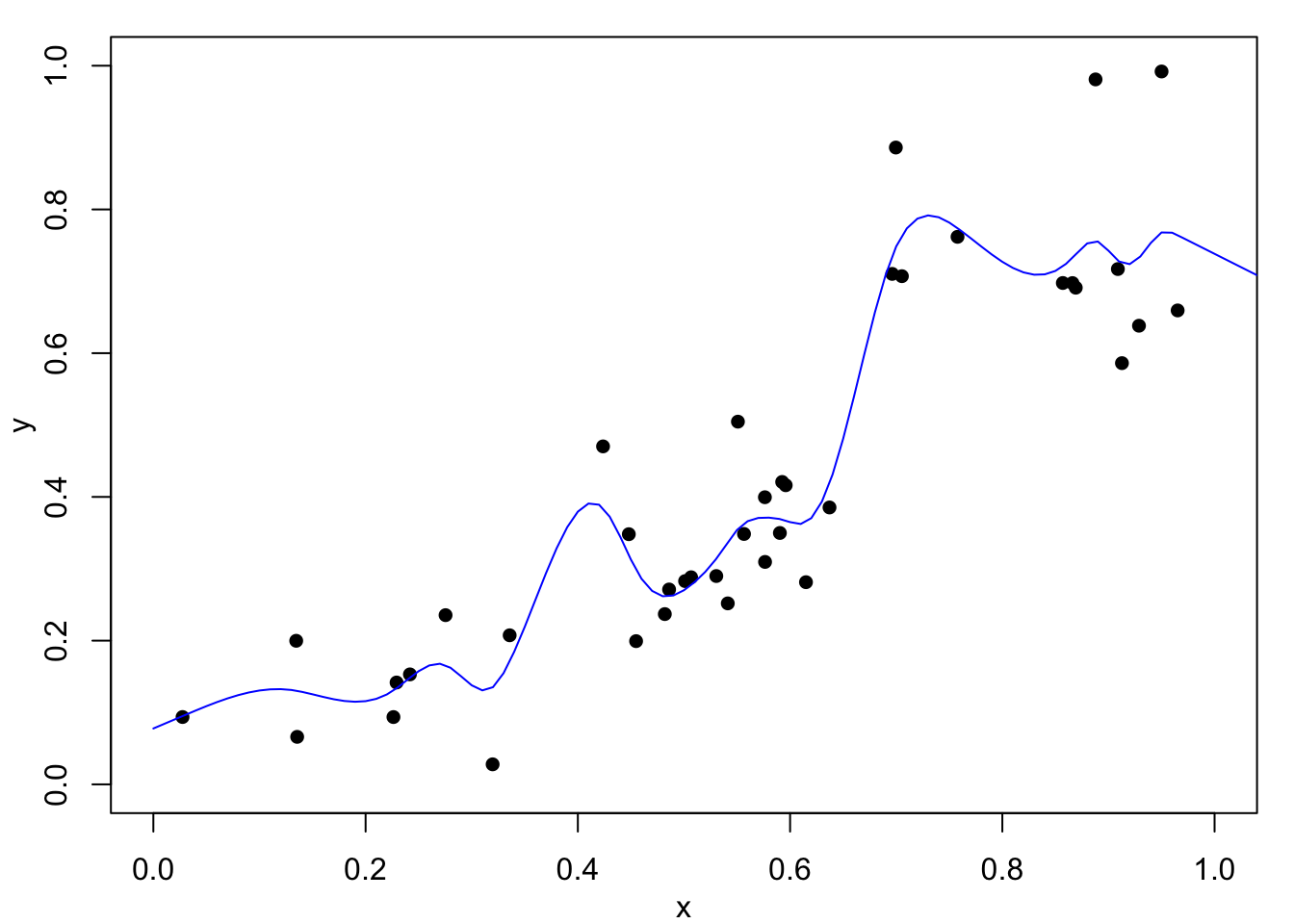

If no value of the smoothing parameter is specified, the the optimal value is calculated using generalised cross-validation as discussed in the next chapter.

4.6 Exercies

4.1 Recall, from MATH3823 Chapter 3, the tropical cyclone data recording the number of cyclones in each of 13 seasons:

Table 4.1: Numbers of tropical cyclones in \(n = 13\) successive seasons¹
Season	1	2	3	4	5	6	7	8	9	10	11	12	13
No of cyclones	6	5	4	6	6	3	12	7	4	2	6	7	4

It is reasonable to allow the average number of cyclones to vary with season, rather than assuming a constant rate.

Fit a cubic smoothing spline to these data, using a range of values for the smoothing parameter \(\lambda\) to estimate the time-varying cyclone rate. By eye, suggest a suitable value for \(\lambda\) and justify your choice. Compare the smoothed estimate of rate with the value obtain by assuming a constant rate.

Follow the R code used in Section 4.5 but don’t worry about finding an exact value for the smoothing parameter, only the order of magnitude.

4.2 Consider the Old Faithful data set on geyser eruptions available in R. Use the following commands to learn more about and visualize the data:

data(faithful)   
help(faithful)  
plot(faithful)

Fit a cubic smoothing spline to these data, using a range of values for the smoothing parameter \(\lambda\). By eye, suggest a suitable value for \(\lambda\).

Taking waiting as the explanatory and eruption as the response, follow the R code used in Section 4.5 but don’t worry about finding an exact value for the smoothing parameter, only the order of magnitude.